Termodinamiğin bir bilim dalı olarak ortaya çıkışı 17. YY İngiltere’sinde buhar makinelerinin icadı ile olmuştur. James Watt’ın bu makineleri geliştirmek için yaptığı çalışmalar ve buharla ilgili daha önceden bilinmeyen özellikleri keşfetmesi, birçok bilim insanının da bu alana yönelmesini sağlamıştır. Latince therme (ısı) ve dynamis (güç) sözcüklerinden türetilen “termodinamik” sözcüğünün ilk tanımını Lord Kelvin “Termodinamizm, cisimlerin bitişik kısımları arasında etkiyen kuvvetler arasındaki ısı ilişkisi ve ısı ile elektrik arasındaki ilişkinin konusudur.” şeklinde yapmıştır. Daha güncel bir tanım yapmak gerekirse de; fiziğin, enerji ve enerjinin şekil değiştirmesi ile uğraşan kolu olarak tanımlayabiliriz. Yani var olan enerjinin başka enerji türlerine dönüşmesinin ısı ile olan ilişkisini anlamamıza yardımcı olur termodinamik. Günlük yaşamda kullandığımız ev eşyalarından, otomobil, uçak ve uzay taşıtlarına, elektrik güç santrallerinden bilgisayarlara kadar, kısaca ısının olduğu bütün uygulama alanlarında termodinamik vardır. Hayatımızda böyle geniş bir yer kaplayan termodinamik, zamanla gelişerek yasalara bölünmüş ve 4 tane yasa oluşturulmuştur.
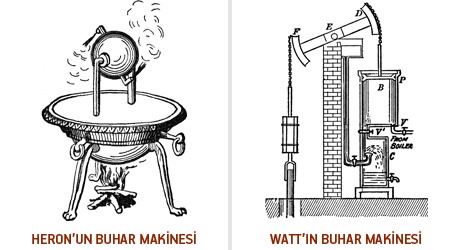
Termodinamiğin 3 Yasası:
Termodinamik ısı ve enerjinin belirli koşullar altında nasıl davrandığını inceleyen bir alandır. Evrendeki olayların çoğunda ısı ve enerji aktarımı gerçekleştiği için termodinamik evrenin anlamayı hedefleyen herkesin öğrenmesi gereken bir konudur. Termodinamiğin evrenin işleyişi hakkındaki ifadesi 4 tane yasa ile özetlenebilir. Bu yasaların bazıları o kadar temel ve basit ki, onları duyduğunuzda “Başka nasıl olacaktı ki zaten?” diyebilirsiniz. Tabi bu yasaları fizik problemlerine uygulamak için üst seviye fizik ve matematik bilmek gerekiyor, ama arkalarındaki temel mantık herkesin kavrayabileceği nitelikte. Yazının bu bölümünde ısı, sıcaklık, ısıl denge, ısı transferi kavramları ile aranızın iyi olduğunu varsayıyoruz.
Sıfırıncı Yasa:
Bu yasanın ne olduğu açıklamadan önce yasaya neden “sıfırıncı” dendiğini izah edelim. Sıfırıncı yasa birinci, ikinci ve üçüncü yasadan sonra Maxwell tarafından ortaya atılmıştır. Diğer üçünden sonra keşfedilmesine rağmen bu yasanın çok daha temel olduğu ve diğer üçünün işlemesi için önkoşul olduğu fark edilince, R.H. Fowler’in önerisi ile yasaya “sıfırıncı yasa” ismi verilmiştir.
Yasanın ifade ettiği şey basit olarak şu; A, B ve C harfleri ile tanımladığımız 3 tane cisim düşünün. C’yi, A ve B’ye ayrı ayrı değdirmemiz durumunda A ile C arasında ve B ile C arasında ısı transferi olmuyorsa, A cismini B’ye değdirmeniz durumunda da A ile B arasında herhangi bir ısı transferi olmaz.
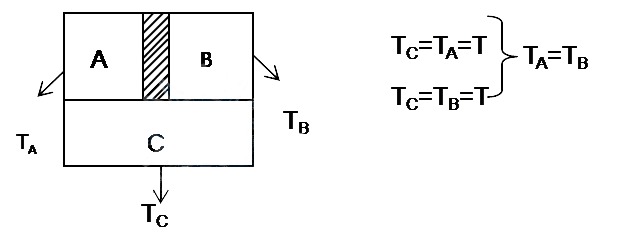
Gündelik bir dille anlatmak gerekirse ısıl dengedeki 2 cismin bir tanesine dokunduğunuzda eliniz yanmıyorsa ikincisine dokunduğunuzda da eliniz yanmaz. Kulağa çok sıradan bir ifadeymiş gibi geliyor fakat “sıcaklık” denen kavramı tanımlamamızı sağlayan yasa sıfırıncı yasadır. Yukarıdaki ifadede C cismini termometre olarak düşünürsek, yasa geçerli olmasaydı A ve B’yi aynı sıcaklıkta ölçmemize rağmen A ve B’nin ısıl dengede olmamaları gibi garip bir durumla karşılaşabilirdik. Aynı sıcaklıkta ölçtüğünüz iki cismin birinden diğerine ısı transferi oluyorsa bu durumda sıcaklık denen kavram tüm anlamını yitirir.
Birinci Yasa:
“Enerji korunumu” denilen kavram hepimize fizik veya kimya dersleri almaya başlamamızdan itibaren defalarca altı çizile çizile sunulur. Birinci yasa da enerji korunumunun yasa ile ifade edilmiş halidir. Gündelik dille “Ne ekersen onu biçersin.” ile ifade edilebilen birinci yasanın resmi ifadesi şudur: Enerji yok edilemez veya yoktan var edilemez fakat bir türdeki enerjiyi farklı enerji türlerine dönüştürmek mümkün.
“Ne ekersen onu biçersin.” sözünü biraz daha açmak gerekirse, bir motor düşünün. Bu motorun çalışarak elektrik enerjisi ürettiğini varsayın. Bu durumda “biçtiğimiz şey” elektrik enerjisi oluyor. Birinci yasanın resmi ifadesine göre motora en az ürettiği elektrik enerjisi kadar başka türden enerji sağlamak lazım çünkü diğer türlü motor yoktan enerji var edecekti. Yani gündelik dille “bir şey ekmek” gerekiyor. Motora sağladığımız enerjinin ne tür olduğunun birinci yasa açısından pek önemi yok, bu enerji rüzgâr enerjisi, nükleer enerji ve daha nice farklı enerji türü olabilir. Birinci yasanın yasakladığı tek şey motora giren enerjiden daha fazlasının çıkmasıdır. Tabi ki tersi de yasak, yani motora enerji sağlamanız durumunda motor hiçbir şey olmamış gibi o enerjiyi yok edemez. İnsanoğlunun asıl derdi enerji yok etmek yerine enerji üretmek olduğu için bu durum “yoktan enerji üretememe” kadar üzücü değildir.
Yüzyıllardır devridaim makinalarının peşinden koşan mucitlerin ölüm fermanıdır bu yasa. Devridaim makinesi kavramını ilk ortaya atanlardan olan Bhaskara’nın yaşadığı yıllardan günümüzde kadar yüzlerce devridaim makinesi yapma girişiminde bulunuldu fakat bu girişimlerden hiçbiri başarılı olmadı. Bundan sonra yapılacak olan girişimler de başarılı olmayacak. Azimli sıçan belki taşı delebilir ama fizik yasalarını delemez.
İkinci Yasa:
Bu yasayı tam anlamak için entropi kavramı ile aranızın iyi olması lazım ve entropiyi bu yazının ileriki bölümlerinde detaylıca anlatacağımız için bu yasaya ileriki kısımlarda daha ayrıntılı değineceğiz. Yasanın resmi ifadesini yazının ileriki kısmına saklayacağız, burada sadece yasanın arkasındaki ana fikri vermek istiyoruz.
Bir bardağı kırdığınızda parçalarının etrafa dağılmasını garip bulmazdınız, fakat o kırılan parçalar rastgele olarak birleşip bardağı tekrar oluştursaydı çok şaşırırdınız. Peki neden? Çünkü bir bardağın parçalarının etrafa dağılmasının birçok yolu vardır. Bir bardak kırıldığında 20 parçaya ayrılırsa, bu 20 parçanın etrafa dağıldığında oluşturabileceği desen sayısı pratik olarak sınırsızdır. Fakat bardağın kırılmadan önceki gibi bütün olmasını sağlayan sadece 1 tane kombinasyon vardır. “Kırık Bardak” durumu için sonsuz tane kombinasyon varken, “Kırık Olmayan Bardak” için sadece 1 tane kombinasyon vardır. Basit olasılık hesabı ile kırık bardağın kırık olmayan bardağa dönüşmesinin olasılığını 1/sonsuz yani 0 olarak bulursunuz. Bu, bir avuç taşı yere atarak taşların şans eseri isminizi ve soy isminizi oluşturmasını beklemek gibidir.
Peki, bunun ikinci yasa ile ne alakası var? İkinci yasa aslında yukarıda anlattıklarımın, evrendeki tüm olaylara genelleştirilmiş hali. İkinci yasaya göre evrendeki her olay evreni öncesinden biraz daha rastgele ve düzensiz yapıyor. Biraz düşünülünce bu çok temel ve basit bir düşünce çünkü evrende herhangi bir şeyin düzenli olmasının sadece birkaç yolu varken düzensiz olmasının sonsuza yakın yolu vardır. Yazının ileriki kısmında bu fikri daha da detaylıca açıklayacağız.
Üçüncü Yasa:
Bu yasayı da anlamak için entropi kavramı ile haşır neşir olmak lazım bu yüzden ikinci yasa ile birlikte bu yasayı da yazının ileriki kısmına saklıyorum. Yasanın basit olarak ifade ettiği şey, mükemmel dizilime sahip bir kristali (moleküllerin dizilimi tamamı ile simetrik) mutlak sıfır olarak kabul ettiğimiz -273,15 derece Celcius’a (0 Kelvin) kadar soğutursak bu kristalin rastsallığı ve düzensizliği 0 olur. Entropi kavramını anlattıktan sonra bu yasayı yeniden ziyaret edeceğiz.
Entropi Nedir?
Öncelikle belirtelim ki bu kavram, popüler kültürde en çok yanlış anlaşılmaya sebebiyet veren kavramlardan birisidir. Çoğu ders kitabı “Entropi düzensizliğin ölçüsüdür.” gibi kısa bir cümle ile durumu geçiştirir. Ama entropiyi sadece bu cümle ile geçiştirmek ona büyük bir haksızlık olur çünkü entropi kavramı insan beyninin ürettiği en derin kavramlardan bir tanesidir. ” Zamanın oku neden geçmişten geleceğe doğrultulmuştur?”, ” Evrenin sonu nasıl olacak?”, ” Yaratmak neden yıkmaktan daha zor?”. Şaşırtıcı gelebilir ama entropiyi tam olarak anladığımızda yukarıdaki 3 soruya da tatminkâr cevaplar vermiş oluyoruz.
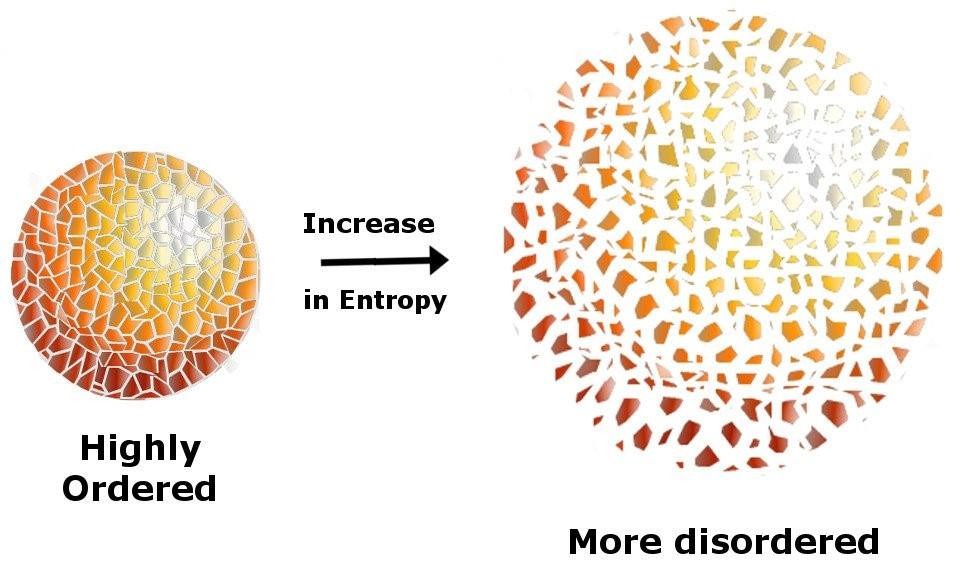
Öncelikle entropi, sıcaklık veya basınç gibi istatistiksel bir özelliktir, yani entropiden bahsedebilmek için elimizde birden fazla parçacık olmalı. Sıcaklık birçok parçacığın (molekül) ortalama kinetik enerjisi olarak tanımlanır. Bu bağlamda, bir tane parçacığın sıcaklığından bahsetmek anlamsızdır. Sıcaklık gibi entropi de çok sayıda parçacık var olduğu zaman anlam kazanmaya başlar. “Çok sayıda parçacık ” olarak tanımladığımız şeye fizikçiler sistem derler. Birçok parçacıktan oluşan herhangi bir varlığa sistem denilebilir. Peki, “parçacık” derken kastettiğim şey ne? Sıcaklıktan veya basınçtan bahsediyorsak “parçacık” kavramına karşılık gelen şey molekül veya atomdur. Fakat entropiden bahsediyorsak “parçacık” herhangi bir şey olabilir. Yani 6 tane zarı alıp her zara “parçacık” diyebiliriz. Bir ülkeye sistem, içinde yaşayan vatandaşlara da parçacık demek mümkündür. Entropinin bu kadar geniş kapsamlı bir kavram olmasının bir sebebi de, parçalardan oluşan herhangi bir şeyin entropisinden bahsedebilmemizdir.
Entropi temel olarak bir sistemin herhangi bir anda bulunabileceği durum sayısını ölçer. Yan yana 5 tane madeni para dizdiğinizi düşününün. Burada her madeni para bir parçacığa tekabül ediyor. Deneyin başında tüm madeni paraları tura olarak ayarladığınızı varsayalım. Bu durumda entropi düşüktür çünkü sistemin bulunabildiği sadece 1 olası durum var, o durum da paraların hepsinin tura olmasıdır. Şimdi madeni paraların sıralamasını bozmadan sırasıyla her parayla yazı tura attığınızı düşünün. İşlem bittiğinde sistemin bulunabileceği durum sayısı kaçtır? Sistemin bulunabileceği durum sayısı 32’dir. Entropinin artmış olduğunu söyleyebiliriz.
Daha da fazla parçadan oluşan bir sistemden bahsedelim. Yazının ilk kısmında kırıldığında 20 parçaya ayrılan bir bardaktan söz etmiştim. Bardak kırılmadan sistemin olası durum sayısı sadece 1’dir, bardağın sağlam olması için 20 parçanın her birinin yerli yerinde olması lazım. Fakat bardağı kırdığımız zaman ortaya inanılmayacak derecede fazla olası durum çıkıyor. Yazının başında da belirttiğim gibi kırılma olayından sonra oluşan parçaların yere dağıldıklarında oluşturabilecekleri desen sayısı çok yüksektir. Bardağın entropisinin arttığı su götürmez bir gerçektir.
Entropiye “düzensizlik” denmesinden pek hoşlanmadığımızı paragrafın başında belirtmiştik (Başka kelime bulamadığımız için yazının başında düzensizlik kelimesini kullanmak zorunda kaldık, bu paragraftan sonra o kelimeyi unutun). Bunun sebebi düzensizliğin nesnel olarak ölçülememesidir. Elinizdeki kalem ile bir kâğıda rastgele 5 basamaklı sayılar yazdığınızı düşünün. İlk bakışta “12345” sayısı “34581” sayısından daha düzenliymiş gibi geliyor. Peki, bir sayının diğerinden daha düzenli olup olmamasını neye göre belirliyoruz? “12345” ardışık rakamlardan oluştuğu için daha düzenli diyebilirsiniz fakat bu durumda plaka numarası “34581” olan birisi de, ikinci sayının kendi plakasıyla aynı olduğu gerekçesiyle “34581” sayısının daha düzenli olduğunu ileri sürebilir. En az sizin kadar da haklı olur. Bu yüzden sistemdeki parçacıkların bir dizilimi herhangi bir diğer dizilimden nesnel olarak daha düzenli değildir. Entropinin ilgilendiği şey dizilimlerin veya desenlerin kendileri de değildir. Siz bir kâğıda 5 basamaklı rastgele bir sayı yazarken yazabileceğiniz olası farklı sayı sayısı 90000’dir. Önemli olan tek şey budur, yazacağınız sayının “12345”‘mi yoksa “32442” olduğunun önemi yoktur. Önemli olan şey sayıyı yazma işlemi sırasında kaç tane olasılığın var olmuş olduğudur. Bu sebepten dolayı bilinçli bir şekilde yazılmış “34581” sayısının entropisi şans eseri olarak yazılmış “12345” sayısından daha düşüktür. Neticede “34581” sayısı bilinçli bir şekilde yazılırsa ortada herhangi bir şans olmaz ve olası durum sayısı 1 olur.
Entropinin Termodinamiğin İkinci Yasası İle Bağlantısı
Şimdi artık ikinci yasanın resmi tanımını verebiliriz: İzole bir sistemin entropisi azalamaz. Bu ifade fiziğin tüm zarafetini ortaya koyuyor. Görünürdeki basitliğinin altında tüm evrenin kaderi yatıyor. Doğruluğunun hiçbir zaman değişmeyeceğine inandığımız ender ifadelerden birisidir ayrıca. Arthur Eddington’un dediği gibi: “Eğer kuramınız Termodinamiğin İkinci Yasası’na karşı geliyorsa hiç ümidi yok demektir, utanç ile yerle bir olması kaçınılmazdır.”.
Üstteki ifadenin ne kadar kutsal olduğunu vurguladık. Peki, bu ifadenin doğruluğundan neden bu kadar eminiz? Üstteki ifade izole bir sistem içinde kendiliğinden gerçekleşen hiçbir olayın o sistemin entropisini azaltamayacağını belirtiyor. Burada izole sistemden kastımız dışarıdan hiçbir şekilde ısı, enerji veya iş almayan bir sistem olmasıdır (evren de izole bir sistemdir). İfadenin sadece izole sistemler için geçerli olduğunu hatırlamak çok önemli. Şimdi izole bir sistemde gerçekleşen herhangi bir olayı düşünelim. Bildiğimiz üzere entropi bu olayın sonucunda gerçekleşmesi olası durum sayısı ile orantılıdır. Durum sayısı 1’den fazla ise entropi artar, tam 1 ise aynı kalır. Bir olay sonucunda entropinin kendiliğinden azalması için bu olay sonucunda gerçekleşebilecek durum sayısının 1’den az olması lazım ki bu imkânsızdır. Yani bir kâğıda rastgele yazabileceğiniz sayı sayısı 0,3 olamaz ama 1000 olabilir. Bu yasanın aslında istatiksel bir çıkarım olduğunu söyleyebiliriz.
Bu yasanın gündelik hayatta çokça karşılaştığımız bir sonucu vardır: Isının sıcak cisimlerden soğuk cisimlere akması. Bariz olmasa da bunun sebebi tamamı ile termodinamiğin ikinci yasasıdır. Bunun tam olarak neden böyle olduğunu anlatmak biraz teknik manevra gerektirir, bu yüzden bir benzetmenin daha yararlı olacağını düşünüyoruz. Bir maddenin sıcaklığının aslında onu oluşturan moleküllerin ortalama kinetik enerjisi olduğunu biliyoruz. Yani sıcak bir maddenin atom başında kinetik enerjisinin soğuk maddeninkinden daha fazla olduğunu söyleyebiliriz. Sıcak ve soğuk bir maddeyi araya getirmek bir yönden yüksek derişimli ve düşük derişimli iki mürekkep çözeltisini karıştırmaya benziyor. Bu analojide derişim ve atom başına kinetik enerji arasındaki benzerliğe dikkat edin. Tabi ki de yüksek derişimli bir çözeltiyi ve düşük derişimli bir çözeltiyi karıştırınca difüzyonun neden yüksek derişimli çözeltiden düşük derişimli olanına olduğunu sorabilirsiniz. Bunun sebebi mürekkep taneciklerinin kaba homojen dağıldığında olası durum sayısının tepe değerine ulaşması. Mürekkep tanecikleri de termodinamiğin ikinci yasasına uyacağı için entropiyi dolayısı ile olası durum sayısını maksimize etmeye çalışırlar. Difüzyonun sıvıyı homojen yapması ise sadece yönün yüksek derişimden düşük derişime olması ile mümkündür. Difüzyon diğer yönde gerçekleşseydi bu entropinin azalmasına yol açardı dolayısı ile ikinci yasa çiğnenmiş olurdu. Aynı argüman iki cisim arasındaki ısı aktarımları için de geçerlidir.
Entropinin Termodinamiğin Üçüncü Yasası İle Bağlantısı
Bu yasanın açıklaması biraz daha kolaydır. İdeal bir kristali 0 Kelvin’e soğutursak o kristali oluşturan parçacıkların hepsi taban durumuna (minimal enerji) düşer ve sıcaklık yükselmediği sürece o durumda kalırlar. Taban durumu sadece 1 tane durum oluşturuyor. Herhangi bir sistemin sahip olabileceği minimum durum sayısı bir olduğuna göre bir maddenin sıcaklığı mutlak sıfıra indiği zaman olası durum sayısı yani entropisi minimuma ulaşır. Bu minimum entropi değeri 0 olarak varsayılmıştır (başka sayı da verebilirlerdi, 0 en mantıklısı duruyor). Buna göre evrende negatif entropiye sahip bir madde de yoktur (bunun için 1’den az durumu olması lazım ki bu imkânsız). Mutlak sıfırın üstünde sıcaklığı olan her maddenin moleküllerinde rastgele titreşimler olur, bu sebepten dolayı entropi de pozitif bir değer alır.
Tersinemez Olaylar ve Zamanın Yönü:
Bir olayın sonucunda evrenin entropisi artıyorsa o olay tersinemezdir. Entropiyi anlatırken verdiğimiz örnekteki olayların hepsi tersinemezdir. Bu olaylara tersinemez denmesinin sebebi olayın sadece tek yönde gerçekleşebilmesidir. Olay bir yönde gerçekleşti mi artık ne kadar beklerseniz bekleyin dışarıda bir müdahale olmadan olay tersine gerçekleşmez. Örnek vermek gerekirse kırık bir bardak 1 milyon yıl bekleseniz de kendiliğinden eski haline dönemez. Tersinemez olayları tespit etmek çok kolay. Bir olayı videoya alın ve videoyu tersten oynatın. Olay gündelik hayatta göremeyeceğiniz şekilde garipse videoya aldığınız olay tersinemezdir.
Fiziğin en temelinde yatan olayların aslında hepsi tersinebilirdir. İdeal ve sürtünmesiz bir ortamda “m” kütleli bir top düşünün. Bu topa bir “F” kuvveti uyguluyorsunuz ve top ivmelenmeye başlıyor. Tüm bu olayı videoya alıp, kaydettiğiniz videoyu tersten oynatırsanız hiçbir gariplik gözünüze çarpmaz. Dolayısı ile ideal ortamda gerçekleşen bu olay tersinilebilir gibi duruyor. Bu durumda bir çelişki yok çünkü entropi ve tersinemezlik zaten ele aldığınız parçacık sayısı arttıkça meydana çıkıyor. Yani sadece 1 tane parçacık üzerine çalışıyorsanız tüm fizik yasaları aslında tersinilebilirdir. Fakat ideal olmayan durumlarda gerçekleşen ve milyonlarca parçacık içeren tepkimeler devreye girince tersinemezlik baskın olmaya başlıyor.
Tersinebilir olaylara bakarak zamanın aslında geriye mi, ileriye mi aktığını kestiremezsiniz çünkü olay iki yönde de sorunsuz bir şekilde gerçekleşebiliyor. Fakat tersinemez olayın sadece geçmişten geleceğe gerçekleşebileceğini bildiğiniz için tersinemez olayların gerçekleşme şekline göre zamanın yönünü tahmin edebilirsiniz. Örneğin cam kırıklarının birleşip tekrar cam bardağını oluşturduğu bir videonun tersten oynatıldığını hemen anlayabilirdiniz.
Entropi ve Evrenin Sonu:
Evren tanımı gereği izole bir sistemdir. Termodinamiğin ikinci yasasını doğrudan evrene uygularsak evrenin entropisinin her an arttığı sonucuna ulaşabiliriz. “İkinci yasa sadece entropinin azalmasını yasaklıyor, bu durumda evrenin entropisi sabit kalıyor olabilir mi?” sorusunu sorabilirsiniz. Cevap hayırdır çünkü entropinin sabit kalması evrende hiç tersinemez olay olmamasını gerektiriyor ki yıldızların ışıması bile tersinemez bir olaydır. Bu yüzden evrenin entropisi her an artmaya devam ediyor. Entropi sonsuza kadar artmaya devam edemez, uzak gelecekte öyle bir an gelecek ki evrendeki tüm enerji, tüm evrene homojen olarak dağılacak (entropi maksimuma ulaşacak). Bu an geldiğinde kullanılabilir hiç enerji kalmayacak, dolayısı ile evrendeki tüm fiziksel olaylar duracak. Buna evrenin ısı ölümü deniyor. Tabii bu olay çok uzak bir gelecekte gerçekleşeceği için şimdilik telaşlanmaya pek gerek yok.
Hazırlayanlar: Timur Öner, Eliz Özön
İTÜ Astronomi Kulübü Üyeleri