Evrenin Nihai Kaderi – I

Okuma Süresi: 13 dakika

İnsanoğlu, ortaya çıkışından itibaren etrafında gözlemlediği olaylar arasında ilişkiler ve örüntüler bularak bu örüntüleri gelecekte olacak olan olayları tahmin etmek için kullanmıştır. Birkaç kez yağmurun gök gürültüsüne eşlik ettiğini gözlemleyen atalarımız, bir süre sonra gök gürültüsünü duyduğu an yağmurun yaklaştığı tahminini yapmaya başladılar. Bu tarz çıkarımları yapmak, insan (ve genel olarak tüm canlıların) beyninin en temel görevlerinden bir tanesidir. Bilim de aslında bu tarz çıkarımları yapmanın daha derli toplu halinden başka bir şey değildir. Bilim sayesinde hiç gitmediğimiz bir yerde, yaşamadığımız zaman dilimi içinde gerçekleşen olayları tarif edebiliyoruz. Bu tarz tarifleri yapmak için  yaptığımız deneyler vasıtasıyla gözlemlediğimiz örüntülerin ve ilişkilerin tüm evren için geçerli olduğunu varsaymamız yeterli. 20.yy’da karadeliklerin doğrudan gözlemlenmemelerine rağmen, teorize edilmesi bu durumun en fazla göze çarpan örneklerinden bir tanesidir.

 Bu yazının asıl amacı evrenin nihai kaderini haber etmekten çok bu tahminlere ne yollar aracılığı ile ulaşıldığını okuyucuya anlatmaktır. Yazının ilk kısmı bu tahminlerin kökünde yer alan teoriyi yüzeysel olarak anlatırken, yazının ikinci yarısı bu teorinin evrenin nihai kaderi hakkındaki tahminleri ile alakalıdır. Yazının çok uzamasının önüne geçmek için bazı kavramların ve yöntemlerin anlatımı, diğer yazılara ve sunumlara bırakılmıştır. Hedef kitleyi arttırma maksadıyla yazıda olabildiğince az formül kullandım fakat anlatımın bütünlüğünü korumak için bir miktar matematik kullanmadan edemedim. Yazının büyük bir kısmını anlamak için lise seviyesi matematik bilgisi yeterli fakat okuyucunun kalkülüs ve diferansiyel denklemler ile tanışık olması yazıda anlatılan matematiksel fikirleri daha çabuk kavramasını sağlayacaktır.

Genel Görelilik ve Friedmann Denklemleri

 Bu yazıda size sunacağım tüm hesaplamalar ve sonuçlar evreni geniş ölçeklerde betimleyen teorilerden en moderni olan genel göreliliğin, gözlemsel verilere uygulanmasıyla elde edilmiştir. Genel göreliliğin ne olduğu hakkında çoğu okurun en azından ufak da olsa fikri vardır. Bu teoriyi okurların kafasında daha da anlaşılır ve belirgin hale getirmek iyi olacak fakat temelinde yatan ağır ama bir o kadar da zarif matematiğe değinmeden bunu sadece belirli bir seviyeye kadar yapabiliriz. Bu tarz zor fikirleri daha anlaşılır seviyeye getirmenin benim açımdan en iyi yolu benzeşimler kullanmaktır. Genel göreliliğin ilkelerini özetleyerek başlayalım.

Genel göreliliğin temelinde Einstein alan denklemleri yatar. Bu denklem, terimlerinin kısa açıklaması ile beraber aşağıda ifade edilmiştir:

Yukarıdaki denklemin ne ifade ettiğini az buçuk anlamak için teorik fizikçi olmaya gerek yok (ama tam anlamak için gerek var). Bu denklem açıkça uzay-zamanın herhangi bir yerindeki enerji yoğunluğunu oradaki uzay-zaman eğriliğine bağlayan deterministik* bir denklemdir. “Uzay-zaman eğriliği” derken neyi kastettiğimizi birazdan daha iyi anlayacaksınız. Diğeri de şudur:

 Lisedeki fizik dersinde defalarca duyduğunuz klasik eylemsizlik yasasının, sonuçları ileride de göreceğimiz üzere çok şaşırtıcı olacak bir modern güncellemesidir yukarıdaki ifade. “Jeodesik” kelimesi aslında düz çizgi ile  eş anlamlı bir terimdir. Yani genel görelilik ile klasik fizik en azından bu konuda mutabık. Genel göreliliği, klasik fizikten devasa bir şekilde ayıran şey ise yukarıdaki ilkelerden ilki.

Konuyu biraz daha derinden anlamak için “ uzay-zamanın bükülmesi” denilen olgunun tam olarak ne olduğuna daha yakından bakmalıyız. Sağduyumuzun bize bu konuda yardım etmesi adına ufak bir deney yapmak, bunu gerçekleştirmek için en kestirme yol olur (yazdıklarımı kafanızda da hayal edebilirsiniz). Elinize boş ve düz bir kağıt alıp, üzerine cetvel yardımı ile düz bir çizgi çekin. Sonra kağıdı çeşitli şekillerde bükün(mümkünse yırtmadan). Başta düz olarak çizdiğiniz çizgi artık eğri büğrü görünecek. Kağıdı uzay-zaman olarak düşünürsek genel göreliliğe göre kağıt büküldükten sonra çizginin bize eğri görünmesinin sebebi çizginin “düz olma” özelliğini kaybetmesi değil, üzerinde çizildiği kağıt parçasının artık eğrilmiş olmasıdır.

 Bu dediğim size çok mantıksız ve soyut geliyorsa bir adım daha derine inmeme izin verin. Bu sefer kağıdı bükmeden önce düz çizgiye ek olarak kağıda bir de kartezyen koordinat sistemi çizdiğinizi varsayın. Çizgiyi de koordinat sisteminin üzerine ve “y=x” denklemine uyacak şekilde çizin. Kağıt, sizin tarafınızdan büküldükten sonra hiç şüphesiz çizgi ve koordinat sistem aynı kağıt üzerinde yer aldıkları için aynı miktarda büküleceklerdir. Büzdüğünüz kağıda dikkatle bakarsanız çizginin hala “y=x” denklemini sağladığını görebilirsiniz. Yani çizgi bize artık eğri görünse de “kağıda göre” çizgi hala y=x denklemi ile tanımlanan düz bir doğrudur.

Bu teoriye neden “genel görelilik” dendiğini şimdi biraz daha iyi kavradığınızı umuyorum. Ne de olsa bir gözlemciye göre düz olan çizgi başkasına eğriymiş gibi görünebilir. İşte jeodesikler de çizildikleri yere göre düz olan çizgilerdir. Uzay-zamanın eğrilmiş (bükülmüş) olduğu başka bir konumdan bakan birisi, bu jeodesikleri düz doğrular gibi değil de eğriler gibi görecektir (bu onların hala düz çizgiler olduğu gerçeğini değiştirmiyor, önemli çizidikleri konuma göre düz olmaları).

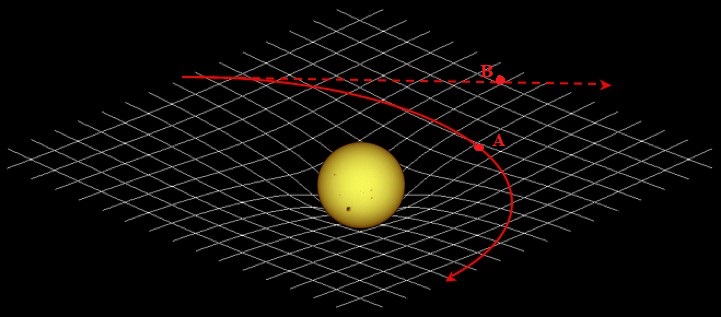
Yukarıdaki görselde beyaz çizgiler uzay-zamanın bükülmemiş olduğu yerdeki bir gözlemcinin “düz çizgilerini” ifade eder. Kırmızı çizgi de yıldızın yanındaki bükülmüş uzayda (yani A noktasında) duran birisinin “düz çizgisini” gösteriyor. Genel göreliliğe göre, cismin uzayda izleyeceği rota A noktasından geçen rotadır.  Bunun fiziksel anlamı ise şudur: Kütleçekimi diye bir kuvvet aslında yoktur. Cisim bir kütlenin etkisi altındayken bile düz çizgiler üzerinden hareket eder. Kütle (veya enerji)’nin** yaptığı şey ise cismi bir kuvvetle çekmek yerine uzay-zamanı büküp düz çizgilerin geometrisini değiştirmektir. Biz insanlar olarak, bükülmüş uzayın geometrisini kafamızda canlandıramadığımız için kütlenin cismi çektiği yanılgısına varırız. Yani kütlelerin ve uzay-zamanın tüm bu karmaşık etkileşimi, temel olarak çok farklı şeyler olsalar da, diğer 3 temel kuvvetle benzer etkiler yaratır.  Yazının konusundan çok fazla sapmamak adına Friedmann denklemlerine geçelim.

Friedmann denklemleri genel görelilik teorisinin tüm evrene uygulanışından başka bir şey değildir. Evrenin her köşesini gezip ölçmeden nasıl olur da tüm evrenin davranışını bir denklemle özetleyebiliriz diye sorabilirsiniz ve bu gerçekten de iyi bir soru olur. Bu sorunun cevabı çok da uzun değil. Evrendeki her yıldız, gezegen ve gökadayı hesaba katamayacağımız doğrudur fakat evrene çok geniş ölçeklerden bakarsak, evrenin aşağı yukarı homojen bir yapıda olduğunu görürüz. Evrenin şeklini, nihai kaderini, yaşını ve genişleme hızını belirleyen de bu geniş ölçekli özelliklerdir. Güneş Sistemi’ndeki gezegenlerin Güneş etrafındaki hareketlerini hesaplamak için nasıl her gezegenin ayrıntılı haritasını bilmemiz şart değilse, aynı şekilde evrenin bir bütün olarak çok uzun zaman ölçeklerindeki davranışını tahmin etmek için her gökadanın konumunu ve kütlesini bilmemiz şart değildir.  İlgilendiğimiz şey sadece geniş ölçekteki ortalama değerlerdir ve evrenin bu bakımdan homojen olduğunu düşünüyoruz (varsayıyoruz). Aşağıda yazacağım denklemdeki terimlerin hepsi, evrenin her köşesinde ortalama olarak aynı değere sahiptir. Homojenlik varsayımı geçerli olmasaydı kozmoloji bilimi belki de bu kadar iyi işleyen bir bilim dalı olmazdı (bir diğer varsayım da izotropiklik varsayımıdır). Aşağıda vereceğim denklem aslında sadece basit bir diferansiyel denklemdir fakat bu onu çözmenin kolay olduğu anlamına maalesef ki gelmiyor.

 Boyut katsayısı (a, eşitliğin sol tarafında olan ve karesi alınan kesrin paydasındaki harf) belirli bir zamandaki evrenin boyutunun, bugünkü boyutuna oranı olarak ifade edilebilir. Bu durumda günümüzdeki evren için a’nın 1 olduğunu otomatik olarak varsaymış oluyoruz. “t0 zamanında a=0.5” demek “t0 zamanındaki evrendeki tüm uzaklıklar orantısal olarak şimdiki evrendeki uzaklıklardan 2 kat daha küçüktü.” demek ile eşdeğerdir. Evrenin tam olarak ne kadar büyük olduğunu bilmediğimiz için (sonsuz da olabilir) evrenin boyutunu oransal olarak ifade etmek gerçekten de mantıklı bir harekettir. İleride bir daha altını çizeceğimiz üzere a=0 durumu Büyük Patlama’yı ifade eder. Eşitliğin sol tarafındaki kesrin payındaki terim ise boyut katsayısının zamana göre türevi yani evrenin genişleme hızıdır. Kesrin kendisi yani evrenin genişleme hızının boyutuna oranı “Hubble parametresi” olarak bilinir ve sanıldığının aksine bir sabit değildir yani zamanla değişir. Günümüzdeki değeri  73.8 (±2.4) km/sn/Mpc’dir. Bu değerin ve diğer kozmolojik değerlerin nasıl ölçüldüklerini anlatmam zaten uzun olan yazıyı daha da uzatacağı için bu konuyu başka bir yazıya saklayacağım.

*Yani bu denklemde(Schrödinger denkleminin aksine) olasılığa yer yok. 

**Göreliliğe göre enerji ve kütle aslında eşdeğer.

Friedmann Denkleminin Fiziksel Anlamı ve Çözümü

 Bu denklemin çözümü a(t) (boyut katsayısının zamana göre fonksiyonu) şeklinde olacaktır. a(t)’yi bilmemiz demek, evrenin herhangi bir zamandaki boyutunu ve genişleme hızını bilmemiz demektir. Bu bilgilerden evrenin yaşını, evrenin gelecekteki durumunu ve ek olarak evrenin birçok diğer özelliğini de çıkarabiliriz. Kısaca a(t) fonksiyonu, evrenin geçmişi ve geleceği hakkında bize çok engin bilgiler sunar. Denklemde var olan tüm sabitlerin ve parametrelerin değerlerini bilseydik denklemin kendisini çözmek çocuk oyuncağı olurdu lakin tahmin edebileceğiniz üzere bu parametrelerin ne olduklarını çıkarmak o kadar da basit ve tekdüze bir iş değildir.

           İhtiyacımız olan bilgiler kısaca şunlardır:

  •   Evrenin eğriliği (K) ve eğrilik yarıçapı (R0).
  •   Evrenin kütle-enerji yoğunluğu (e(t), yine zamanla değişen bir değer).

“Kütle-enerji” ifadesini kullanmamızın nedeni, genel göreliliğe göre kütlenin ve enerjinin temel olarak aynı şey olmalarından geçiyor (E=mc^2 formülü). Kütle-enerji yoğunluğu diğer bir değişle birim hacme düşen enerji miktarıdır (kulağa geldiği gibi karmaşık bir kavram değil). Evrenin geniş ölçeklerde homojen olduğunu varsaydığımız için teoride de olsa evrendeki toplam enerjiyi evrenin toplam hacmine bölerek kütle-enerji yoğunluğunu elde edebiliriz. Tabii bulduğumuz değer sadece 100 Mpc* veya daha geniş ölçekler için doğru olacaktır (alttaki notu okuyun). Evrenin eğriliği ise evrenin geniş ölçekteki geometrisi ile alakalıdır. Evrenin eğriliği konusunu da diğer yan konular gibi başka bir yazıya saklayacağım.

Önemli Not: Yazının başında da vurguladığımız gibi evrenin homojen olduğunu ve her zaman homojen kalacağını varsayıyoruz. Yani K, e(t) gibi parametreler sadece zamanın bir fonksiyonudur. Tabii ki de kütle-enerji yoğunluğu ve eğrilik konum değiştikçe ufak da olsa dalgalanmalara maruz kalır fakat bu ufak dalgalanmalar kozmolojik açıdan önemsizdir. Biz de, Dünya ve Güneş Sistemi olarak, bütün evrenin bakış açısından bakılırsa çok ufak bir enerji dalgalanmasıyız.

*Megaparsek, 1 Mpc=1 milyon Parsec=3.26 milyon ışık yılı

Evrenin Eğriliği ile Kütle-Enerji Yoğunluğu Arasındaki İlişki

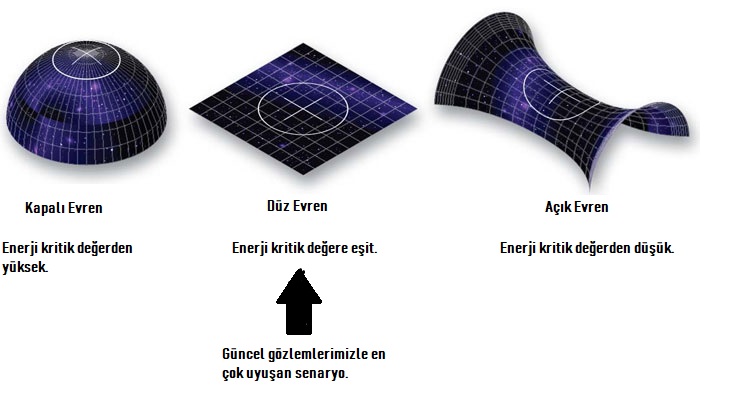
Evrenin eğriliğinin tam olarak ne olduğunu daha açıklamadığım için şimdilik yaptığım hesapların fiziksel anlamı üzerinde çok kafa yormayın. Friedmann denklemine biraz daha dikkatli bakarsak K değerinin, e(t) ve H0 (evrenin günümüzdeki hali için ölçülen hubble sabiti)’a doğrudan bağlı olduğunu görürüz. K=0 değerini kritik değer olarak kabul edersek (ki bu değer düz geometrili bir evreni ifade ediyor) K’nın kritik değerde olduğu durumlar için aşağıdaki gibi bir bağıntı elde ederiz:

H0’nün değerinin  defalarca ölçülmüş olduğunu biliyoruz (WMAP uydusu bu ölçümlerden birisini gerçekleştirmiştir). Evrenin eğriliğinin de aynı şekilde, çeşitli gözlemler sonucunda, kritik değer olan 0’a çok yakın olduğu tespit edilmiştir. Bunlar kısaca şu anlama geliyor: gözlemlerin ve teorinin uyuşması için evrenin enerji yoğunluğunun belirli bir değerde olması gerekiyor. Bu değer “kritik kütle-enerji yoğunluğu” olarak bilinir ve tam olarak hangi değerde olması gerektiği yukarıdaki hesaplarda belirtilmiştir. Evrenin enerji-kütle yoğunluğunun, geometrisini dikte etmesi başta şaşırtıcı görünse de şaşılacak bir durum yok: sonuçta kullandığımız denklem genel görelik kullanılarak türetildi ve genel görelilik, kütle-enerji ile evrenin eğriliğini doğrudan birbirine bağlayan bir teoridir. Enerjinin kritik değerden farklı olması durumunda evrenin geometrisi de çok temel bir şekilde farklı olacaktır.

Yazı dizisinin ikinci ve son kısmını buradan okuyabilirsiniz.

Hazırlayan: Timur Öner

İTÜ Astronomi Kulübü Üyesi

Kaynaklar:

Yorumlar kapatıldı.

WordPress gururla sunar | Theme: Baskerville 2 by Anders Noren.

Yukarı ↑